Как одним отрезком из треугольника сделать три треугольника

Система игр и упражнений для знакомства детей старшего возраста с геометрическими фигурами, их элементами и свойствами. Система игр и упражнений для знакомства детей старшего дошкольного возраста с геометрическими фигурами, их элементами и свойствами.

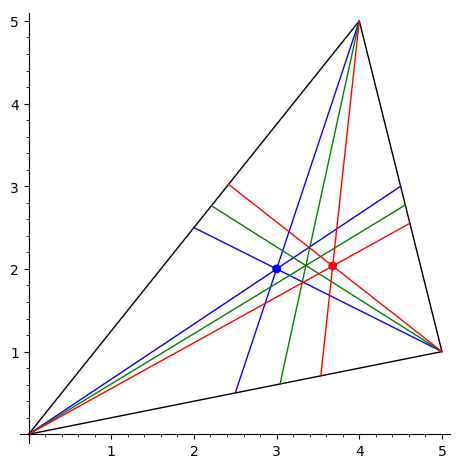
Разбиение на подобные треугольники

Нам то и дело приходится выступать в роли наставников. Иногда это профессия, иногда помощь своим детям, учащимся в школе или университете, а бывает так, что желание поделиться чем-то красивым с неофитами может перерасти в призвание. В любом из этих случаев нам нужны хорошие примеры.

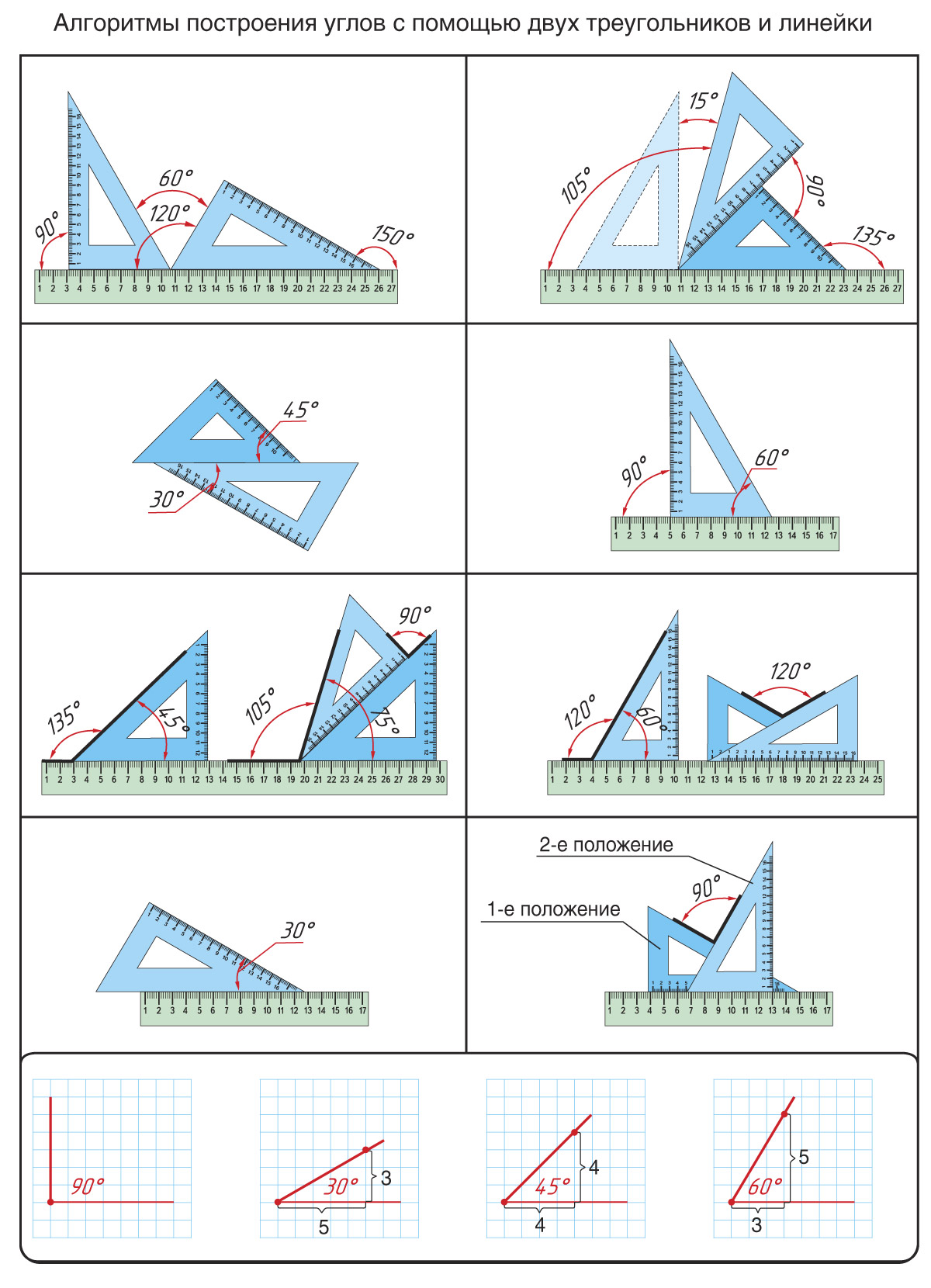
Не каждая геометрическая фигура может похвастаться таким количеством линий, как треугольник: медиана, средняя линия, биссектриса, высота, серединный перпендикуляр. В этот раз поговорим про среднюю линию и узнаем, зачем она нужна. Треугольник — это геометрическая фигура, которая получилась из трех отрезков.

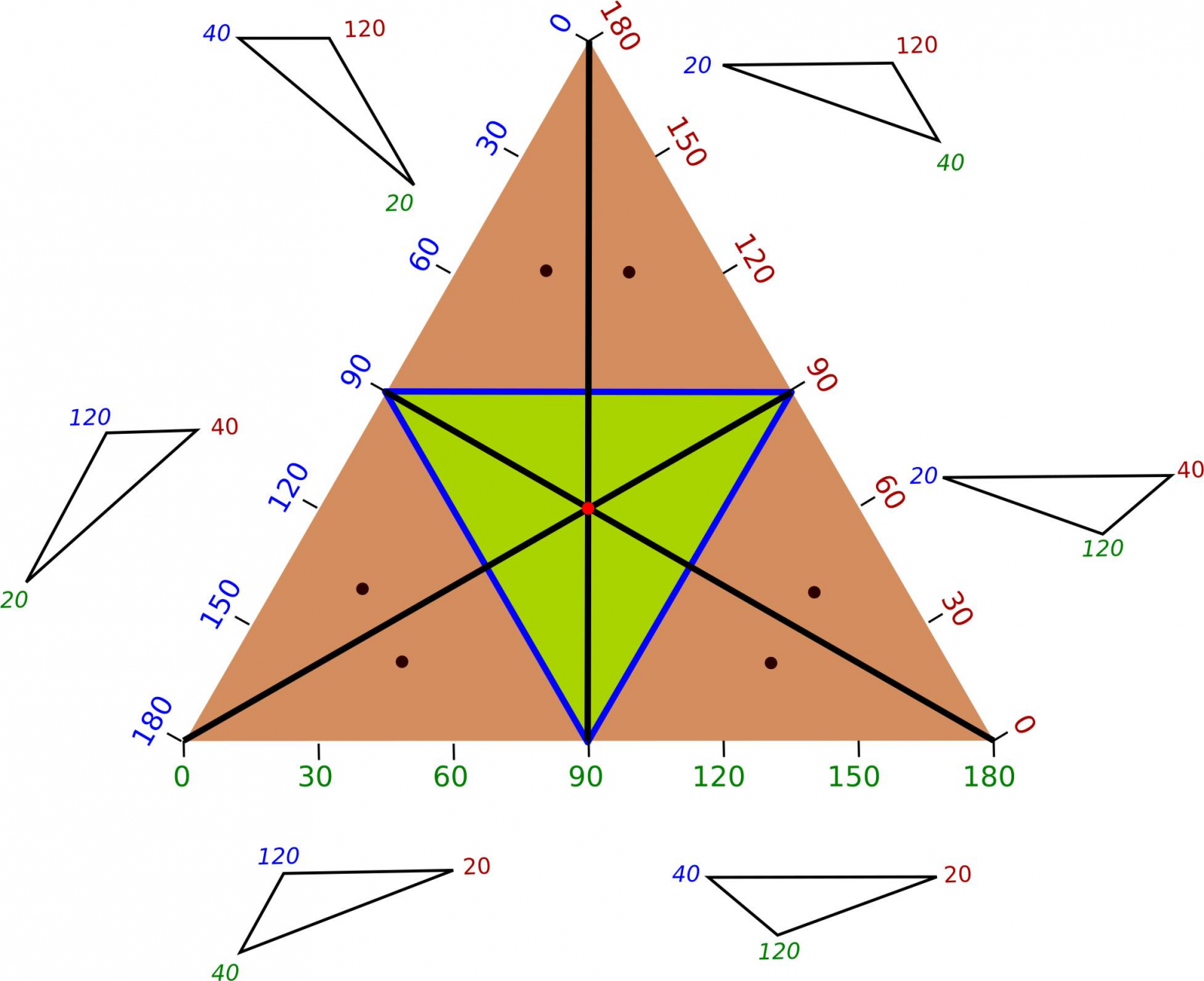
Длины биссектрис треугольника Легко построить треугольник по длинам трёх его медиан. Чуть сложнее построить треугольник по длинам его высот. Задача о восстановлении треугольника по длинам его биссектрис намного труднее и интереснее. Решена она была совсем недавно. На русском языке это впервые опубликовано в первом номере «Кванта» за год. Оказывается, никаких ограничений на длины биссектрис нет!

Похожие статьи

• Модные игрушки для девочек 5 лет
• Новогодняя игрушка снеговик из ниток своими руками
• Модный утепленный костюм
• Ремонт триммеров хускварна своими руками